The Role of Working Memory in Math Processing

Why is math so difficult?

Because “doing math” is not a unitary skill.  It involves a long list of cognitive abilities, on each of which children vary widely in terms of abilities.

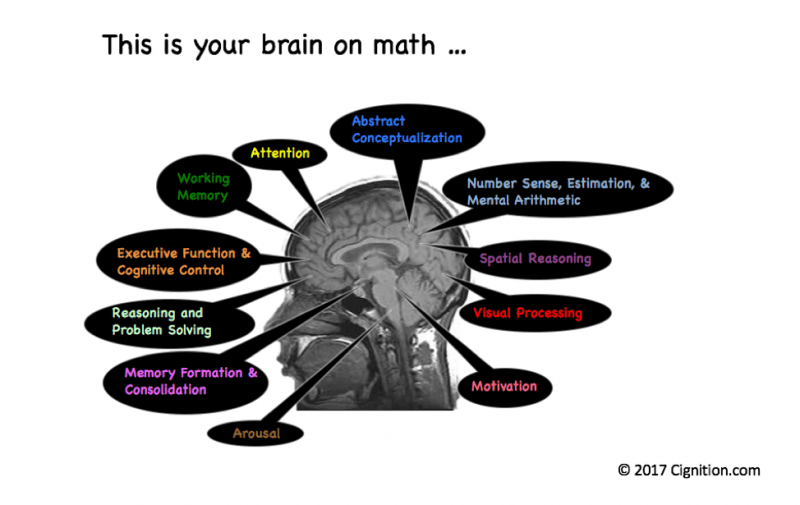
Mathematical processing requires:

• Various forms of attention (focused, inhibition, shifting, multitasking)
• Working memory – mental sketchpad where information can be manipulated (auditory and visuospatial)
• Abstract conceptualization – imagining and interpreting non-observable concepts
• Number sense, estimation, & mental arithmetic – processing mathematical information and having a conceptual understanding of symbolic numbers and their relationships
• Spatial reasoning – processing the size, location, orientation, and movement of objects in space.
• Visual processing – thinking about, comparing, relating, interpreting, or imagining visual information
• Motivation – desire to work on math tasks
• Arousal – positively valenced arousal may result in excitement about math whereas negatively valenced arousal may be math anxiety
• Memory formation & consolidation – encoding new mathematical information, incorporating information into pre-existing conceptual schemas, and retrieval of learned information
• Reasoning and problem solving – logical thinking based on premises
• Executive function & cognitive control – organizing and sequencing information, planning, imagining multiple scenarios and outcomes, and strategizing.

Difficulties within a single cognitive domain that is required for math will make it difficult for children to perform mathematical computations.  One that is particularly significant is working memory, which is a mental sketchpad that allows individuals to hold separate pieces of information in their mind while performing some kind of manipulation on it.  To demonstrate the role of working memory in math, consider the following finding:

According to an NCMT report, 50% of 8^th graders have difficulty with this question:

Order these according to quantity.

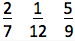
How would you go about doing this?  Take a minute and think about what cognitive processes you may be recruiting to resolve a problem like this (for example keep track of any mental imagery you are bringing up to compare these, and keep track of how much information you are keeping track of as you go along)

In order to solve this, most people:

• Need to imagine a visuospatial mental representation of quantity for each item (e.g., a number line, fraction bars, fraction circles, area model, parts of a whole, etc.)
• Have to keep track of at least 2 positions of quantity in their working memory (including the visuospatial model associated with that fraction and the quantity it represents) while computing location of the third

This is quite a bit of information to hold in mind, particularly for children whose working memory is not as developed that that of an adult, and particularly for children who have difficulty with working memory.

It is important to note that conceptual knowledge makes a difference:

• Quickly identifying that 5/9 is more than half while the other two are less than half can help order the largest quantity
• Knowledge that the combination of a smaller numerator and larger denominator means a smaller quantity helps identify the smallest quantity
• Individuals with more expertise have developed a “number sense” and can get an approximation of the quantity of each number almost immediately

A student who does not have conceptual fluency would need to perform a number of mental calculations and visuospatial computations and likely to make errors. The less conceptual understanding a student has, the more working memory they would need to process the problem, which can become a vicious cycle: low working memory leads to poor understanding which requires more working memory.

Cignition is taking a proactive approach to deal with this problem.  First, the amount and type of working memory required for each conceptual leap is pre-identified, and then the information is used to develop in-game scaffolds that act as a “mental sketchpad”.   The scaffolds can be geared towards ability levels and used when necessary.  The goal is to support working memory and other cognitive functions that are related to the math task but not required for understanding the concept.  This takes out a lot of the cognitive effort so that students can focus their mental resources on understanding the concepts.  This way students can achieve a deep conceptual understanding of the mathematical concepts regardless of their working memory or other cognitive abilities.  Once students have learned the concepts the scaffolds are no longer used to ensure that students are able to complete the entire process without assistance and gain efficiency with procedural fluency.

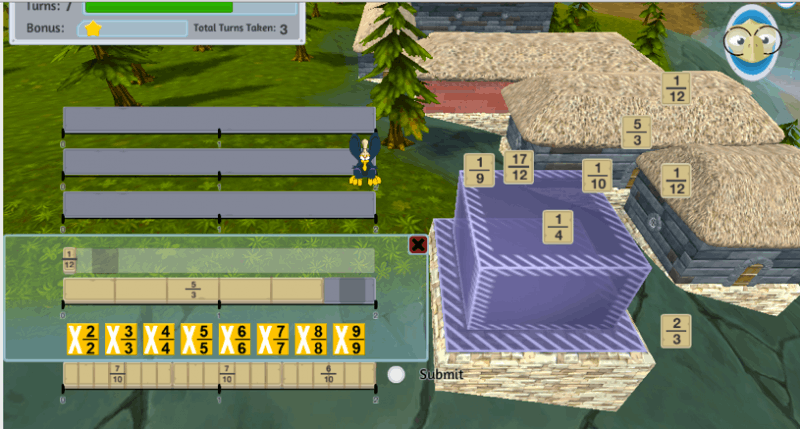
One example of these scaffolds is the “sketchpad” used for creating buildings:

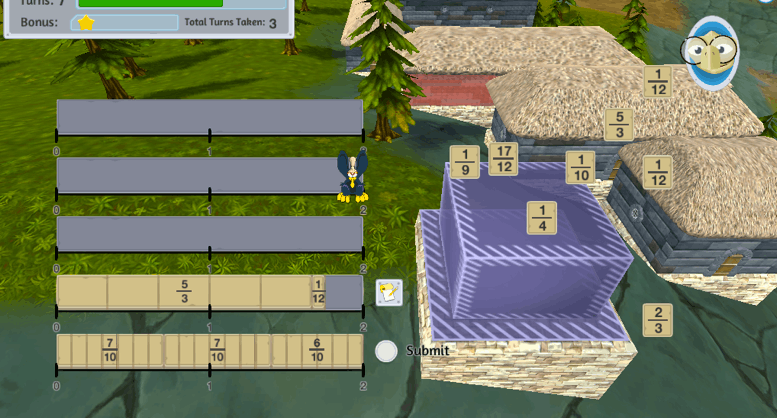
The player has placed a 5/3 brick on the second row and a little friendly monster flew in to place a 1/12 brick beside it. The player must now place the final brick to complete the row and will therefore have to add the two fractions.  The conceptual leap here is that the denominators will have to match before we add the two numerators together.

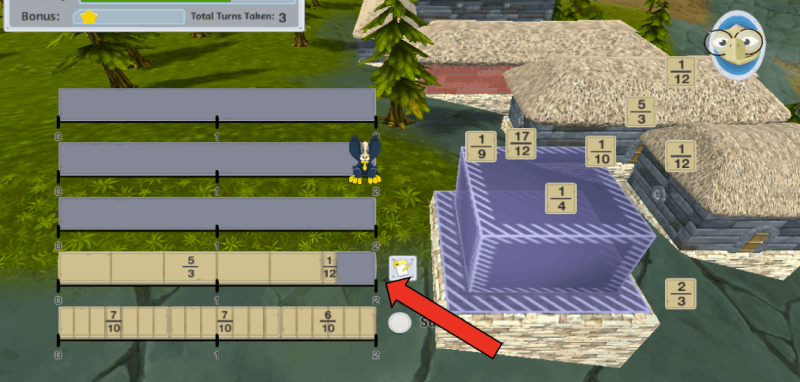
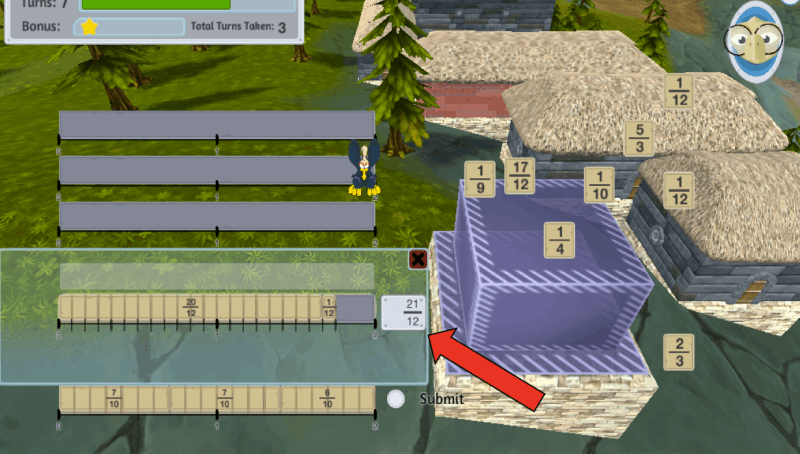
Students must first realize that the first fraction has to be multiplied by 4/4 to match denominators with the second fraction, and then perform those calculations in their mind, hold the result of multiplying the numerator in their working memory (5 x 4 = 20 → 2 digits), while keeping track of the denominator (12 → 2 + 2 digits = 4 digits), add the two numerators and keep track of the sum (20 + 1 = 21).  Before they can release the other digits held in their working memory they must revisit them and realize that they do not need them anymore.  Moving forward, they must consider the fraction as a whole by first recalling the denominators (12) and numerator (21) and subtracting to obtain the current fraction 1 9/12, which they will need to simplify to 1 3/4 (this not only takes up the working memory required for keeping the 7 digits listed here – the average working memory space for most adults – but also requires additional working memory slots as comparisons and calculations are performed to get from the first fraction to the second).  Students must then subtract the value they have from the value they need (2 – 1 3/4 = 1/4), which also requires a number of working memory slots depending how proficient they are with fractions.  This is exhausting!

Many of the numbers can be “chunked” once students are more familiar and proficient with fractions and they can also use math fact retrieval for many items rather than having to compute each one.  The problem is that teachers who are extremely proficient with these computations and fractions may not realize how much cognitive resources students who do not understand the concepts would need to process this information.  It would also be very challenging (if not impossible) for the teacher to know the precise extent of working memory spaces each person requires as a result of their combined conceptual understanding, working memory capacity, math fact retrieval proficiency, and other related cognitive abilities.

In this game, students have the option to click on a button and open a “sketchpad”, which performs the computations for them and holds the numbers in their “workspace”.  These computations are the supportive skills that are not immediately required to understand the mathematical concepts in this exercise.  This way, students can focus on the conceptual methods of what needs to be done to solve this problem.  More importantly, a visuospatial workspace is provided that the students can manipulate and interact with to develop a deeper and richer representation of the concepts. Having the visuospatial representations available when new math concepts are being encoded increases the likelihood that the representations will also be retrieved next time the student thinks about the concept.  The ability to retrieve such a rich representation of a concept can have a major impact on the amount of working memory that may be required for future tasks involving this concept and helps prepare the brain for future as it can facilitate the way that students integrate new information into their pre-existing schemas of math concepts that involve richly connected multiple perspectives.

In this example, students need to determine which whole number must be multiplied to make the denominators similar while the sketchpad will do the calculations for them.  They can then see the denominator change and match with the second denominator.  They can also get a sense of how much space each fraction takes up and how this remains the same despite the change in denominators (due to the corresponding change in the numerator).

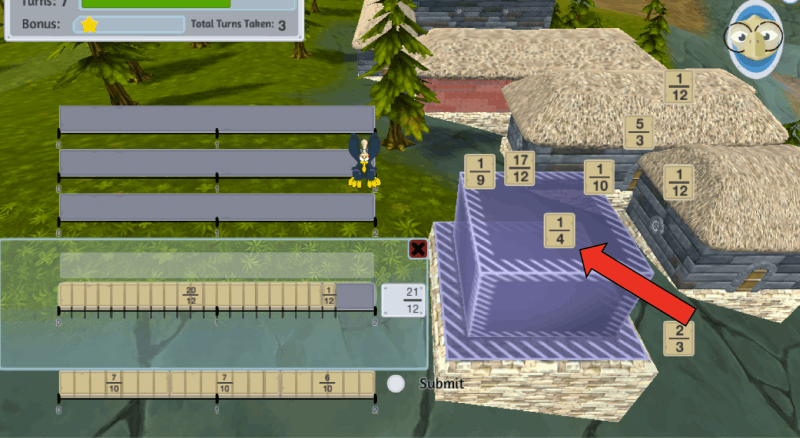
They can drag the bricks around to get a visual understanding of how much space each fraction takes up on the number line, as well as a better estimate of the amount that remains.  An important goal of this procedure is to help students develop a stronger sense of estimation and number senseto make educated guesses and also to check their work.

Once the students have made an estimation about which brick remains they can look to the available bricks and see if it exists.  This is also where the game can catch their misconceptions and provide in-game tutorials if they demonstrate that they are missing or inaccurately interpreting a concept.

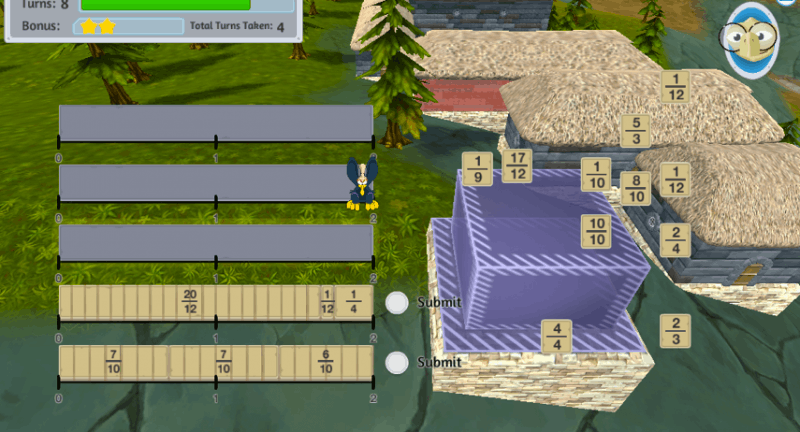
Not having the cognitive abilities to fully understand math concepts can result in missing or inaccurate information and frustration, as well as a dislike of math or math anxiety.  Recognizing the cognitive demands of a task for different students and supporting them through carefully placed scaffolds can be a highly effective method for ensuring that every student can achieve a deep understanding of the mathematical concepts regardless of their skill level with other cognitive functions.  Once concepts are understood, students can devise multiple ways of solving a problem, where some routes may be less cognitively challenging for them than others.

National Council of Teachers of Mathematics (2007) The Learning of Mathematics: 69^th NCTM Yearbook. Reston, VA: National Council of Teachers of Mathematics.